Precedence: Chapter 3

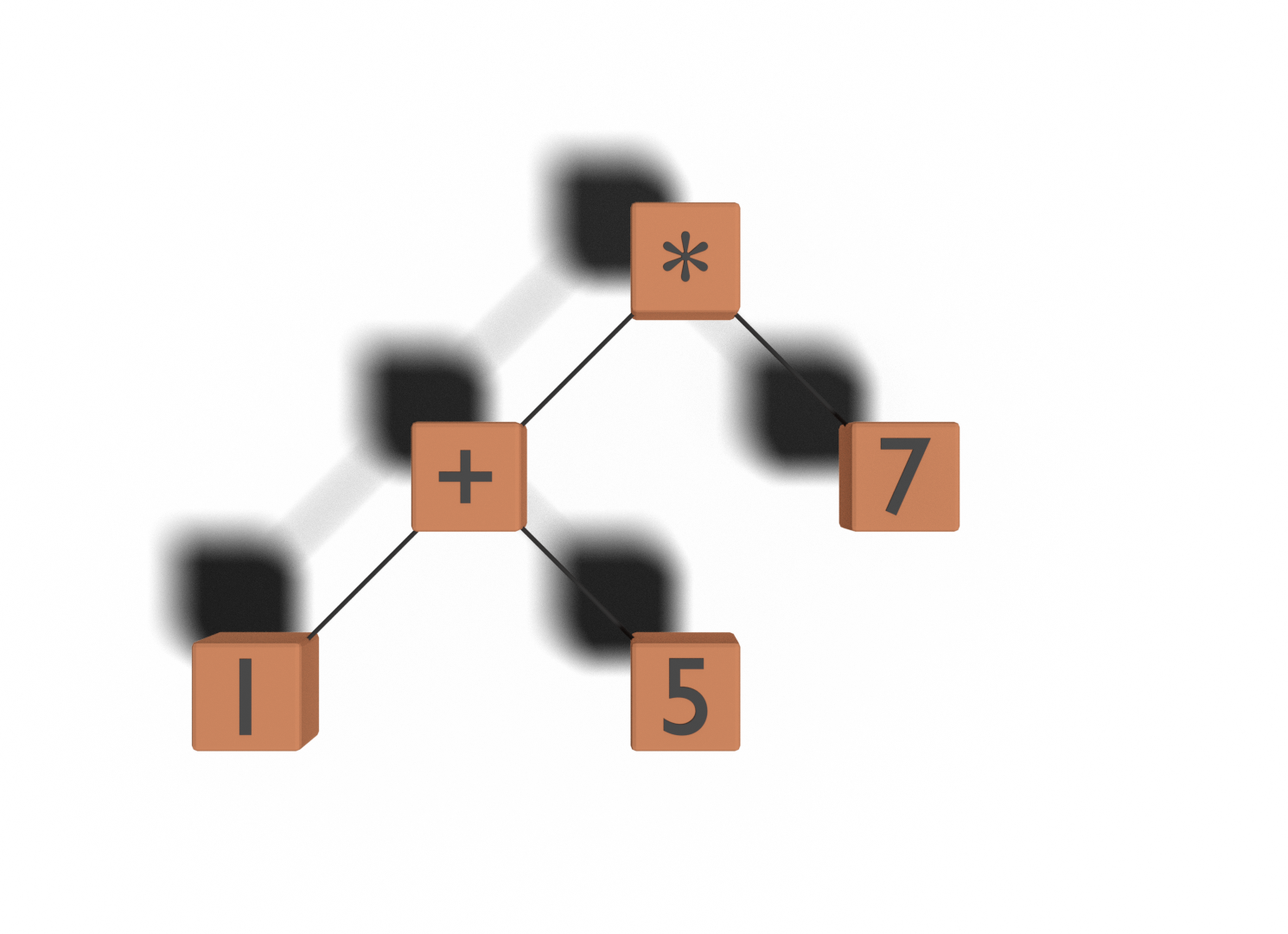
If you haven’t already, I highly recommend putting on the deep thinking music of your choice (I like this), and pondering this one for a while. Try and figure out what’s actually going on here. We parse an expression, like, 1 + 5 * 7, and it becomes a tree:

And we evaluate it, following the simple rules of evaluation, and get an entirely wrong answer. There’s a bug somewhere, but where? Is it parsing? Tree construction? Evaluation?

Find the Root Cause

When I’m trying to figure out the cause of a bug, I like to go through each step very slowly and methodically and try to find the one step where we went off course. Luckily, if you’ve been following along, we’ve already covered the exact point at which our algorithm failed. Recall that our wrong answer was 42. And to get 42, we multiplied 7 and 6, but if you look at the expression 1+ 5 * 7, and evaluate it with the order of operations, at no point will you multiply 7 and 6. You should multiply 5 and 7, get 35, and add 1 to it to arrive at the correct answer of 36.

So why did our algorithm multiply 6 and 7? Because it added 1 and 5 first! Ah-hah! Multiplication is supposed to be before addition. And why did we perform the addition first? Because it was lower in the tree, and we always evaluate lower nodes first (recall that left and right are evaluated before self).

We’re getting somewhere. So we’ve discovered the issue, but we could solve it in two places. We could either put the multiplication lower in the tree than the addition, or we could change our evaluation routine. Both of these options are completely valid, and each of them have their own pros and cons, but we decided to go with the first option to keep our evaluation routine as clean as possible.

Let’s go through our parsing exercise again, except this time, we’ll push higher precedence operators lower in the tree. Let’s take a slightly more complex expression.

Fix the Problem: a Step by Step Guide

Alright, we’ve done 1 + 5 before, it looks like this:

Now we hit a ‘*’.

It is higher priority than a ‘+’, so it has to be pushed down:

Whoa, what just happened!? Let’s break it down. First, we appended our ‘*’ 7 normally. But we know that tree is wrong, because it means that the ‘+’ will be evaluated first. So, the solution is to push the ‘*’ further down the tree. It has to move down the right side to preserve the right-to-left-ness of the expression, and a ‘*’ needs a left and a right child, so it kidnaps ‘+’s right child (things said about ‘children’ in a programming context can sometimes be horrific) and keeps it for itself. Watch the animation a few times, and you can see all this action happening. It’s like a Michael Bay film. I should’ve added explosions.

If you think about it, this actually makes perfect sense, because, at the end of the day, the ‘+’ won’t operate on the 5, it will operate on whatever the result of 5*7 is, which is more accurately captured in this tree. So, in a way, this tree is a more accurate representation of the expression than the other tree (which is part of the reason we decided to go with this solution instead of changing our evaluation rules).

Okay, now that we’re armed with this knowledge that we need to push higher precedence operators further down the tree, let’s parse the rest of the expression:

And there you have it! If you evaluate this tree using the simple rules from above, you will arrive at the correct answer. We’re all done!

The End?

Not so fast. So far, this has all been a thought exercise. We’ve drawn some pretty pictures and talked about our problems and some potential solutions, but we haven’t written a single line of code. At the end of the day, a man’s only as good as his running executable, so in the next chapter, we’ll put our money where our mouth is and write up a working solution to this! Stay tuned.